Sistemas de actuación
Capitulo ocho
Mecánica
Objetivos
Después de estudiar esto capítulo, el lector debe ser capaz de:
Determinar los posibles sistemas de actuación mecánica para la transmisión de movimiento entre los que están lineal a rotatorlo, rotatorlo a rotatorio, rotatorio a lineal y transmisión de movimiento cíclico.
Evaluar las capacidades de acoplamientos, levas, engranes, trinquete, bandas de transmisión,
Impulsores do cadena y cojinetes para sistemas de actuación
son útiles para obtener movimientos que varíen en la forma que se desea En
este capítulo se presentan las características básicas de algunos mecanismos.
Muchos de los efectos que antes se obtenían con el uso de mecanismos
la actualidad se logran mediante sistemas de microprocesadores. Por ejemplo:
Antes en las lavadoras domésticas se utilizaban levas montadas en un eje
racional para lograr una secuencia de acciones sintonizadas como abrir una
válvula para dejar pasar agua al tambor, cerrar el suministro de agua, encender
un calentador, etcétera. En las lavadoras modernas se utiliza un microproce
sador que se programa para que produzca las salidas deseadas en la secuencia
requerida. Otro ejemplo es la rueda de balance de resorte helicoidal con en-
granes y manillas de un reloj que en la actualidad son reemplazados en gran
parte por un circuito integrado tal vez con una pantalla de cristal líquido. El
enfoque de la mecatrónica da como resultado una simplificación, y a menudo
la reducción de costos.
8.1-Sistemas mecánicos
Este capítulo aborda el tema de los mecanismos, es decir, dispositivos que se pueden considerar convertidores de movimiento, en tanto transforman el movimiento de una forma a otra. Por ejemplo, con un mecanismo, un movimiento lineal se puede convertir en un movimiento rotacional; un movimiento en una dirección convertirse en uno con otra dirección en ángulo recto respecto al primero; un movimiento lineal alterno en uno rotacional, como en el motor de combustión interna, donde el movimiento alterno de los pistones se convierte en el del cigüeñal y éste, a su vez, lo transfiere al eje de la transmisión.
Entre los elementos mecánicos están los
mecanismos de barras articuladas, levas, engranes, piñón y cremalleras, cadenas,
bandas de transmisión, etcétera. Por ejemplo; el arreglo piñón y cremallera
convierte un movimiento rotacional en uno lineal; los engranes con eje paralelo
reducen la velocidad de un eje; los engranes cónicos transmiten movimiento
rotacional en un ángulo de 90°; una banda dentada o una cadena de transmisión
transforman el movimiento rotacional de un eje en el movimiento de otro eje;
las levas y las barras articuladas son útiles para obtener movimientos que
varíen en la forma que se desea. En este capitulo se presentan las
características básicas de algunos mecanismos.
Muchos de los efectos que antes se
obtenían con el uso de mecanismos en la actualidad se logran mediante sistemas
de microprocesadores. Por ejemplo, antes en las lavadoras domesticas se utilizaban
levas montadas en un eje rotacional para lograr una secuencia de acciones
sincronizadas como abrir una válvula para dejar pasar agua al tambor, cerrar el
suministro de agua, encender un calentador, etcétera. En las lavadoras modernas
se utiliza un microprocesador que se programa para que produzca las salidas
deseadas en la secuencia requerida. Otro ejemplo es la rueda de balance de
resorte helicoidal con engranes y manillas de un reloj que en la actualidad son
remplazados en gran parte por un circuito integrado tal vez con una pantalla de
cristal liquido. El enfoque de la mecatrónica da como resultado una
simplificación, y a menudo la reducción de costos.
No obstante, los mecanismos todavía son útiles en los sistemas mecatrónicos. Por ejemplo, el sistema mecatrónico de las cámaras fotográficas automáticas que ajusta la apertura para obtener una exposición adecuada usa un mecanismo que ajusta el tamaño del diagrama.
Si bien la electrónica hoy día se utiliza en forma generalizada para desempeñar diversas funciones que antes se realizaban con mecanismos, estos todavía son útiles para llevar acabo funciones como las siguientes:
1. Amplificación de fuerzas, como la que dan las palancas.
2. Cambio de velocidad; por ejemplo, mediante engranes.
3. Transferencia de rotación de un eje a otro; por ejemplo, una banda síncrona.
4. Determinados tipos de movimiento, como los que se obtienen mediante un mecanismo de retorno rápido.
El termino cinemática se refiere al estudio del movimiento sin tener en cuenta las fuerzas. Al analizar los movimientos sin considerar las fuerzas o energías, se dice que se hace el análisis cinemático de un mecanismo. Este capítulo es una introducción a este tipo de análisis.
8.2 Tipos de movimiento
El movimiento de un cuerpo rígido se puede considerar como la combinación de movimiento de traslación y rotación. Al considerar las tres dimensiones espaciales, el movimiento de traslación seria un movimiento que se divide en componentes que coinciden con uno o más de los tres ejes. (Figura 8.1 a)). Un movimiento de rotación puede ser una rotación con componentes que giran alrededor de uno o más de los ejes. (Figura 8.1 b)).

Los movimientos complejos suelen ser la combinación de movimiento de traslación y rotación. Por ejemplo, el movimiento para levantar con la mano un lápiz que esta sobre una mesa. Esto puede involucrar que oriente la mano en determinado angulo con la mesa, gira la mano, separe los dedos y los coloque en la posición adecuada para tomar el lápiz. Esta es una secuencia de movimientos bastante complejos. Sin embargo, es posible separarlos en combinaciones de movimientos de traslación y rotación . Este tipo de análisis es relevante no cuando movemos una mano humana, si no cuando damos instrucciones a un robot para que realice una tarea. En este caso, es necesario separar el movimiento en una combinación de movimientos de traslación y rotación para diseñar mecanismos que ejecuten estos componentes de movimiento. Por ejemplo, entre la secuencia de señales de control que se envían a un mecanismo podría figurar agrupamientos de señales con las cuales se instruye a la articulación 1 girar 20° y a la articulación 2 hacer una extensión de 4 mm de movimiento de traslación.
8.2.1 Grados de libertad y de restricción
Un aspecto importante del diseño de los elementos mecánicos es la orientación y disposición de elementos y partes. Un cuerpo que está libre en el espacio se desplaza en tres direcciones mutuamente perpendiculares e independientes y gira de tres maneras alrededor de estés direcciones (Figura 8.1).
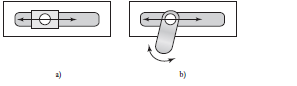
Se dice que este cuerpo tiene seis grados de libertad. El número de grados de libertad es el número de componentes de movimiento requeridas para generar el movimiento. Si una articulación está limitada a desplazarse a lo largo de una línea, sus grados de libertad de traslación se reducen a uno. La Figura 8.2a) muestra una articulación que sólo tiene este grado de libertad de traslación. Si la articulación está limitada a desplazarse en un plano, entonces tiene dos grados de libertad de traslación. La Figura 8.2b) ilustra una articulación que tiene un grado de libertad de traslación y un grado de libertad de rotación.
Figura 8.2.1 GRADOS DE LIBERTA Y DE RESTRICCION
Uno de los problemas más importantes del diseño es reducir la cantidad de grados de libertad, lo cual requiere un número y orientación idónea de las restricciones. Si no hay restricciones, un cuerpo tendría seis grados de libertad. Se asigna una restricción por cada grado de libertad que no se desea. Suponiendo que no hay restricciones redundantes, el número de grados de libertad sería igual a 6 menos el número de restricciones presentes. Sin embargo, las restricciones redundantes son frecuentes, de modo que para las restricciones de un cuerpo rígido se cumple la regla básica:
6 número de restricciones – número de grados de libertad -número de redundancias
Por lo tanto, si se desea que un cuerpo esté fijo, es decir, que tenga cero de grados de libertad, y si no se introducen restricciones redundantes, el número de restricciones necesarias es seis. Un concepto que se utiliza en disco es el principio de la restricción mínima, el cual establece que al fijar un cuerpo o al guiarlo en determinado tipo de movimiento, debe emplearse la cantidad mínima de restricciones, es decir, no deben existir redundancias. Con frecuencia esto recibe el nombre de diseño cinemático. Por ejemplo, para definir una flecha que sólo gire alrededor de un eje, sin movimiento de traslación, hay que reducir a 1 el número de grados de libertad. Por lo tanto, 5 es la cantidad mínima de restricciones para hacerlo. Cualquier restricción adicional sólo producirá redundancias. El montaje que se utilizará para montar la flecha tiene un cojinete de bolas en un extremo y de un cojinete de rodillo en el otro (Figura 8.3). Este par de cojinetes impide el movimiento de traslación en dirección perpendicular al eje y y la rotación alrededor del eje z y el eje y. El cojinete de bolas impide el movimiento de traslación en el eje x y el eje z. Por lo tanto, en total hay cinco restricciones. Es decir, sólo queda un grado de libertad para la rotación requerida en torno al eje x. Si en ambos extremos de la flecha se coloca un cojinete de rodillos, entonces los dos cojinetes impiden el movimiento de traslación en el eje x y el eje z, lo que implicaría una redundancia. Esta redundancia podría causar daño. Si en ambos extremos de la flecha se utilizan cojinetes de bola, entonces, para evitar redundancias, el anillo de rodamiento de uno de los cojinetes no se fija en su cubierta para permitir cierto grado de deslizamiento en una dirección axial.

8.2.2 Carga Los mecanismos son estructuras y, por lo tanto, transmiten y soportan cargas. Para determinar las cargas que soporta cierto elemento es necesario hacer un análisis. Después se evalúan las dimensiones del elemento para que su fuerza y, quizá su rigidez, sean suficientes para soportar esas cargas.
8.3 Cadenas cinemáticas
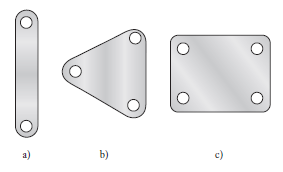
Cuando se analizan los movimientos de un mecanismo sin prestar atención a las fuerzas, dicho mecanismo puede considerarse como una serie de articulaciones individuales. Cada parte del mecanismo que se mueve en relación con otras se denomina articulación. Ésta no tiene que ser un cuerpo rígido, basta que sea un cuerpo resistente capaz de transmitir la fuerza requerida con una deformación despreciable. Por este motivo, en general se representa como un cuerpo rígido con dos o más puntos de unión con otras articulaciones que se llaman nodos. Cada articulación puede desplazarse en relación con sus articulaciones vecinas. La Figura 8.4 muestra ejemplos de articulaciones con dos, tres y cuatro nodos. Una articulación es una conexión de dos o más articulaciones en sus nodos, la cual permite que haya cierto movimiento entre las articulaciones conectadas. Las palancas, el eje del cigüeñal, la biela y los pistones, las guías de deslizamiento, las poleas, correas y ejes son ejemplos de articulaciones.
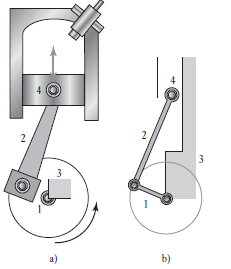
Una secuencia de piezas de articulación y articulaciones se conoce como cadena cinemática. Para que una cadena cinemática transmita movimiento, una articulación debe estar fija. El movimiento de una articulación produce movimientos relativos predecibles en las demás. Al variar la articulación que se mantiene fija es posible obtener diversos mecanismos a partir de una misma cadena cinemática. Un ejemplo de cadena cinemática es el motor de un automóvil, donde el movimiento alterno de un pistón se transforma en el movimiento rotacional de un eje de cigüeñal montado en un marco fijo (Figura 8.5a)). Esto se puede representar como cuatro articulaciones conectadas (Figura 8.5b)). La articulación 1 es el cigüeñal, la articulación 2 la biela, la articulación 3 el sistema articulado fijo y la articulación 4 la guía de deslizamiento, es decir, el pistón, que se desplaza en relación con el sistema articulado fijo (vea mayores detalles en la sección 8.3.2)
El diseño de muchos mecanismos se basa en dos formas básicas de cadenas cinemáticas, la cadena de cuatro barras y la cadena biela-corredera-cigüeñal. Los siguientes son ejemplos de las formas que estas cadenas pueden adoptar.
8.3.1 Cadena de cuatro barras
La cadena de cuatro barras consiste en cuatro acoplamientos conectados entre si de manera que producen cuatro piezas de articulación alrededor de las cuales pueden girar. La Figura 8.6 muestra variantes de esta cadena obtenidas al modificar las longitudes relativas de las articulaciones. Si la suma de la longitud de la articulación más corta más la longitud de la más larga es menor o igual que la suma de las longitudes de las otras dos articulaciones, por lo menos una de las articulaciones podrá completar una revolución respecto al acoplamiento fijo. Si la condición anterior no se cumple, ninguno de los acoplamientos podrá realizar una revolución completa. Ésta se conoce como condición de Grashof. En la Figura 8.6a), el acoplamiento 3 está fijo y las longitudes relativas de los acoplamientos son tales que los acoplamientos 1 y 4 pueden oscilar, pero no girar. El resultado es un mecanismo de doble palanca. Al acortar el acoplamiento 4 en relación con el 1, el acoplamiento 4 puede girar (Figura 8.6b)) con el acoplamiento 1 oscilando, y el resultado anterior se conoce como mecanismo palanca-cigüeñal. Los acoplamientos 1 y 4 tienen la misma longitud y ambos pueden girar (Figura 8.6c)); lo que se obtiene se conoce como mecanismo de doble cigüeñal. Al modificar el acoplamiento fijo se obtienen otros mecanismos.

La Figura 8.7 ilustra cómo aprovechar el mecanismo anterior para avanzar la película en una cámara de cine. Conforme el acoplamiento 1 gira, el extremo del acoplamiento 2 se engancha en una de las perforaciones de la película, la jala, la suelta, avanza y retrocede para quedar nuevamente enganchado en la siguiente perforación.
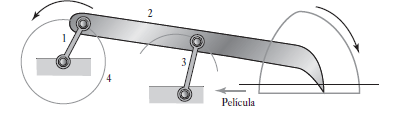
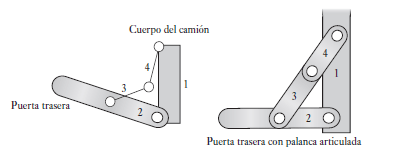
Algunas piezas de articulación tienen posiciones de palanca articulada, en las cuales la articulación no reacciona ante las entradas de sus acoplamientos. La Figura 8.8 ilustra esta palanca articulada, una articulación que controla el movimiento de la puerta trasera de un camión de manera que cuando el acoplamiento 2 queda en posición horizontal ninguna carga adicional en el acoplamiento provocará otro desplazamiento. Hay otra posición de palanca articulada en este acoplamiento: cuando los acoplamientos 3 y 4 están en posición vertical y la puerta trasera está en posición vertical.
8.3.2 Mecanismo biela-corredera-cigüeñal
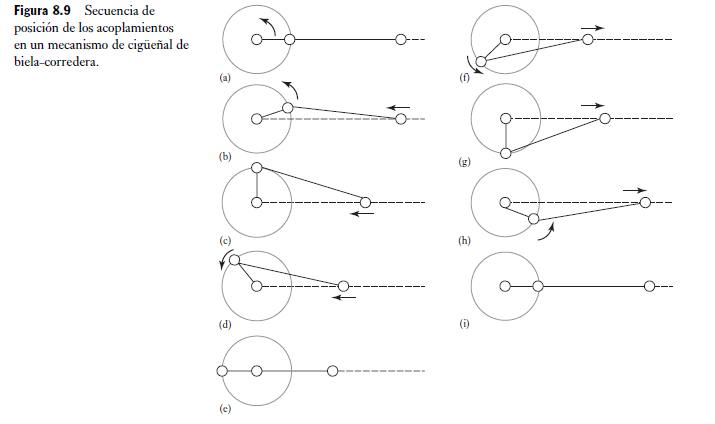
Este mecanismo consta de un cigüeñal, una biela y una corredera como el que presenta la Figura 8.5 que corresponde a un motor simple. En esta configuración el acoplamiento 3 está fijo, es decir, no hay movimiento relativo entre el centro de rotación del cigüeñal y la cubierta en la que se desplaza el pistón. El acoplamiento 1 es el cigüeñal que gira, el acoplamiento 2 la biela y el acoplamiento 4 la corredera que se desplaza en relación con el acoplamiento fijo. Cuando el pistón se desplaza atrás y adelante, es decir, cuando el acoplamiento 4 se desplaza atrás y adelante, el acoplamiento 1, o cigüeñal, se ve obligado a girar. De esta manera, el mecanismo se transforma en una entrada de movimientos atrás y adelante que se transforma en un movimiento rotacional. La Figura 8.9 muestra varias etapas de este movimiento. Una manera útil de ver cómo se debe comportar cualquier mecanismo es construir a escala un modelo en cartulina y mover los acoplamientos. El cambio en la longitud de un acoplamiento hace entonces que se determinen los cambios en el comportamiento del mecanismo.
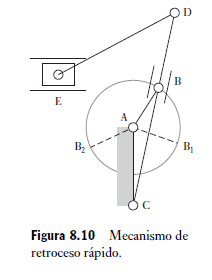
La Figura 8.10 presenta otra modalidad de este mecanismo, un mecanismo de retroceso rápido, este consiste en un cigüeñal en rotación, el acoplamiento AB, el cual gira alrededor de un centro fijo; una palanca oscilatoria CD la cual hace que gire en torno a C por el deslizamiento del bloque B a lo largo de CD en cuanto AB gira, y un acoplamiento DE que hace que E se desplace hacia adelante y hacia atrás. E puede ser el carro de una máquina y contenga una herramienta de corte. El carro estará en los extremos de su movimiento cuando las posiciones del cigüeñal sean AB¹ y AB². De este modo, conforme al cigüeñal se mueve en sentido contrario al de las manecillas del reloj, de B¹ a B², el carro hace un recorrido completo, la carrera de corte. Si el cigüeñal gira a una velocidad constante dado que el ángulo de rotación cigüeñal requerido para el recorrido de corte es mayor que el ángulo para el recorrido de retroceso, el recorrido de corte consume más tiempo que el recorrido de retroceso, de donde le viene el concepto de mecanismo de retroceso rápido. Un modelo de cartulina y diagramas similares pueden construir como los que se presentan en la Figura 8.9.
8.4 Levas
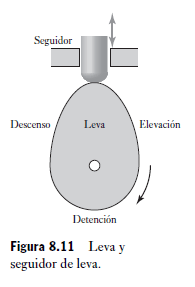
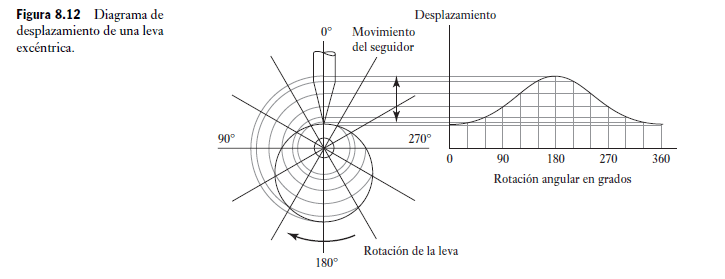
Una leva es un cuerpo que gira u oscila y, al hacerlo, transmite un movimiento alterno u oscilatorio a un segundo cuerpo conocido como seguidor, con el cual está en contacto (Figura 8.11). Al girar la leva, el seguidor sube, se detiene y desciende; los lapsos correspondientes a estos pasos dependerán de la forma de la leva. La sección de elevación de la leva provoca el ascenso del segui dor y de su perfil dependerá qué tan rápido se eleve el seguidor. La sección de descenso de la leva permite el descenso del seguidor y de su perfil dependerá qué tan rápido desciende. La sección de detención de la leva permite que el seguidor permanezca en un mismo nivel durante un tiempo considerable. La sección de detención de la leva es donde es circular y su radio no cambia. La forma requerida de leva para que se produzca un movimiento en particular del seguidor dependerá de la forma de la leva y del tipo de seguidor que utilice. La Figura 8.12 muestra el tipo de diagrama de desplazamiento del seguidor que se puede producir mediante una leva excéntrica cuyo seguidor sea de punta o de cuchillo. Ésta es una leva circular con un centro de rotación desfasado. Esto produce una oscilación del seguidor, la cual es un movimiento armónico simple y que se usa a veces en bombas. La distancia radial desde el eje de rotación de la leva hasta el punto de contacto de la leva con el seguidor da el desplazamiento del seguidor con respecto al eje de rotación de la leva. La figura muestra cómo las distancias radiales, y de aquí los desplazamientos del seguidor, varían con el ángulo de rotación de la leva. El diagrama de desplazamiento vertical se obtuvo tomando la distancia radial de la superficie de la leva a partir del punto de rotación en diferentes ángulos y proyectándolos alrededor para que se den los desplazamientos en dichos ángulos.
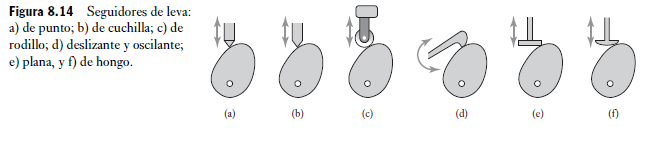
La Figura 8.13 muestra los tipos de diagramas de desplazamiento del seguidor que pueden producir con otras diferentes formas de levas y cualesquier seguidores, de punto o de cuchilla. La leva en forma de corazón (Figura 8.13a)) proporciona un desplazamiento de seguidor que se incrementa a una velocidad constante con el tiempo antes de disminuir a una velocidad constante con el tiempo, de donde se da una velocidad uniforme al seguidor. La leva en forma de pera (Figura 8.13b)) proporciona un movimiento estacionario al seguidor de alrededor de media revolución de la leva y se eleva y cae de manera simétrica en cada uno de los restantes cuartos de revolución. Este tipo de leva se utiliza en control de válvulas de motores. La detención mantiene abierta la válvula en tanto que la mezcla de aire y combustible pasa al cilindro. Cuanto más grande sea la detención, es decir, cuanto mayor sea la superficie de la leva con un radio constante, más tiempo tiene el cilindro para cargarse por completo con vapores inflamables. La Figura 8.14 muestra varios ejemplos de diversos tipos de seguidores de leva. Los de rodillo se construyen principalmente de bolas o de rodillos. Su gran ventaja es la baja fricción con respecto al contacto deslizante, aunque tienen un costo mayor. Los seguidores de cara plana tienen más demanda por ser más económicos y se pueden fabricar en tamaños más pequeños. Se utilizan mucho en levas de válvulas de motor. Aunque se pueden usar en seco, se les suele lubricar e incluso pueden estar sumergidas en aceite.

8.5 Engranes
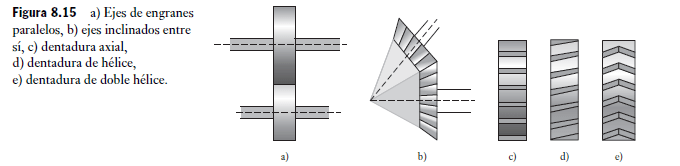
Los trenes de engranes son mecanismos muy utilizados para transferir y transformar el movimiento rotacional. Se emplean cuando se necesita un cambio en la velocidad o en el par motor de un dispositivo que está girando. Por ejemplo, la caja de velocidades de un auto permite al conductor igualar los requerimientos de velocidad y par motor para cierta superficie con la potencia disponible del motor. Los engranes transmiten el movimiento rotacional entre ejes paralelos (Figura 8.15a)) y entre ejes inclinados entre sí (Figura 8.15b)). El término engrane cónico se usa cuando las líneas de los ejes se intersecan, como se observa en la (Figura 8.15b)). Cuando dos engranes están dentados, el mayor se llama corona o engrane y el menor piñón. Los engranes que se usan para conectar ejes paralelos tienen dientes rectos, es decir, los ejes se cortan en líneas axiales paralelas al eje (Figura 8.15c)). Este tipo de engrane se conoce como engrane recto. Una variante es la que tiene dientes helicoidales, los cuales se cortan en forma de hélice (Figura 8.15d)) y se conocen como engranes helicoidales. Éstos ofrecen la ventaja de un engranado gradual de los dientes y, por lo tanto, la transmisión en los dientes es más suave y su vida se prolonga más. Sin embargo, la inclinación de los dientes respecto al eje produce una componente de fuerza axial en el cojinete del eje. Para eliminarla se utiliza una doble hilera de dientes helicoidales (Figura 8.15e)). Considere dos engranes conectados, A y B (Figura 8.16). Si el engrane A tiene e 40 dientes y el B 80 dientes, el engrane A gira dos veces en el mismo tiempo o que el engrane B gira una vez. Por lo tanto, la velocidad angular del engrane A, vA, debe ser el doble de la del engrane B, vB, es decir: vA vB = número de dientes en B número de dientes en A= 80 40 = 2 Dado que la cantidad de dientes de un engrane es proporcional a su diámetro, se tiene que: vA vB = número de dientes en B número de dientes en A= dB dA Por lo tanto, en este caso, el engrane B debe tener dos veces el diámetro del A. El término relación de engranaje designa la relación entre las velocidades angulares de un par de engranes conectados. En el ejemplo, esta relación es 2.

8.5.1 Trenes de engranes
El término tren de engranes describe una serie de engranes conectados entre sí. El término tren de engranes simple se aplica a un sistema en el que cada uno de sus ejes sólo tiene un engrane, como en la Figura 8.17. En este caso, la relación de engranaje total, es la relación entre las velocidades angulares entre los ejes de entrada y salida y, por lo tanto, es igual a vA/vC.
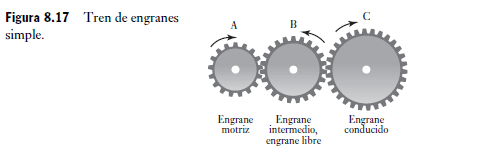
G =
Considere un tren de engranes que consta de los engranes A, B y C, como en la Figura 8.17. El engrane A tiene 9 dientes y C, 27. Ahora bien, dado que la velocidad angular de un engrane es inversamente proporcional a la cantidad de dientes, la relación de engranaje es 27/9 = 3. El efecto del engrane B es sólo modificar la dirección de rotación del engrane de salida respecto a la que tendría si sólo los engranes A y C estuvieran conectados. El engrane intermedio B, se denomina engrane libre. Esta ecuación para la relación de engranaje total G se puede reescribir como
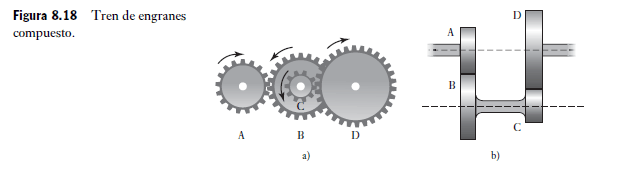
Pero vA/vB es la relación de engranaje del primer par y vB/vC es la del segundo par. Por lo tanto, la relación de engranaje total de un tren de engranes simple es igual al producto de las relaciones de engranaje de cada par sucesivo de engranes. El término tren de engranes compuesto se refiere a un tren de engranes cuando dos de ellos están montados en un eje común. En la Figura 8.18a) y b) se muestran dos ejemplos de este tren de engranes. El tren de engranes de la Figura 8.18b) permite que los ejes de entrada y salida estén en línea.
Figura 8.18 Tren de engranes compuesto.
Cuando dos engranes están montados en el mismo eje, su velocidad angular es igual. Por lo tanto, para los dos trenes de engranes compuestos de la Figura 8.16, vB = vC. La relación de engranaje total G es, por lo tanto,
G =
vA vD
=
vA vB
*
vB vC
*
vC vD
=
vA vB
*
vC vD
En el arreglo de la Figura 8.16b), para que los ejes de entrada y de salida estén alineados, es necesario que los radios de los engranes cumplan lo siguiente: rA + rB = rD + rC
Considere un tren de engranes compuestos como el de la Figura 8.18a), donde A, el engrane motriz, tiene 15 dientes; B, 30 dientes; C, 18 dientes y D, el engrane conducido, 36 dientes. Dado que la velocidad angular de un engrane es inversamente proporcional al número de dientes, la relación de engranaje total es:
G =
30 15 *
36 18 = 4
Por lo tanto, si la entrada en el engrane A es una velocidad angular de 160 rev/ min, la velocidad angular de salida del engrane D es 160/4 = 40 rev/min. Un tren de engranes simple, sea de engranes de dientes rectos o helicoidales, o engranes cónicos, por lo general está limitado a una relación de engranaje total de casi 10. Esto se debe a la necesidad de mantener el tren de engranes en dimensiones manejables a fin de mantener la cantidad de dientes de la rueda de piñón arriba de cierto número mínimo, en general entre 10 y 20. Para obtener relaciones de engranaje mayores se utilizan trenes de engranes compuestos porque la relación de engranaje es igual al producto de cada uno de las relaciones de engranaje de los conjuntos de engranes paralelos.
8.5.2 Movimiento rotacional a movimiento de traslación
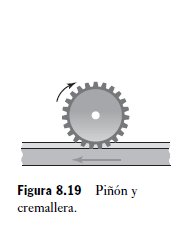
El piñón y cremallera (Figura 8.19) es otra forma de engranaje, que es en esencia dos engranajes Inter bloqueados uno con una base circular del radio infinito. Tales engranajes se pueden utilizar para transformar ya sea un movimiento lineal a uno rotatorio o un movimiento rotatorio a un movimiento interlineal. Otro método que se ha empleado para convertir un movimiento rotatorio en uno de traslación es el sistema de tornillo y tuerca. Con la forma convencional de tornillo y tuerca, la tuerca gira y se mueve a lo largo del tornillo estacionario. Sin embargo, si el tornillo se gira en la tuerca, adjunta a la parte a ser conducida, la tuerca se mueve a lo largo de la rosca. A este arreglo se le conoce como tornillo de avance. El avance L es la distancia de movimiento paralelo al eje del tornillo cuando se le da una vuelta a la tuerca; para una rosca simple el avance es igual al paso. En n revoluciones la distancia de movimiento en paralelo al eje del tornillo será nL. Si se completan n revoluciones en un tiempo t, la velocidad lineal v paralela al eje del tornillo es nL/t. Como n/t es la cantidad de revoluciones por segundo f para el tornillo, entonces:
v [1]
nL t
[1] fL
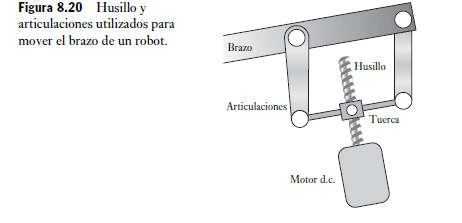
Sin embargo, hay problemas al utilizar este tipo de arreglo para convertir el movimiento de rotación en un movimiento lineal ya que hay fuerzas de alta fricción implicadas en el contacto de deslizamiento directo entre el tornillo y la tuerca, así como con la falta de rigidez. El punto de la fricción se puede resolver si se utiliza un husillo. Este tipo de tornillo es idéntico en principio al tornillo de cabeza, pero los cojinetes de bolas se ubican en la tuerca del tornillo. Este arreglo se ha usado en robots para manejar el brazo, que funciona con un motor de c.d (Figura 8.20). El motor hacer girar el tornillo, que a su vez mueve la tuerca hacia arriba o hacia abajo. El movimiento de la tuerca se transmite al brazo mediante una articulación.
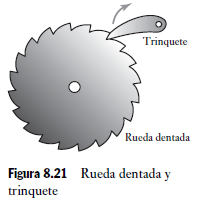
8.6. Rueda dentada y Trinquete
Los trinquetes se utilizan para trabar un mecanismo cuando sostiene una carga. La Figura 8.21 muestra una rueda dentada y un seguro. Este mecanismo consta de una rueda dentada, con dientes en forma de sierra que se enganchan con un brazo denominado trinquete. El brazo está sujeto a un pivote que se mueve hacia atrás y hacia adelante para trabar la rueda. La forma de los dientes es tal que sólo permite la rotación en una dirección. El trinquete impide la rotación de la rueda dentada en el sentido de las manecillas del reloj y sólo puede hacerlo levantando el seguro, el cual casi siempre se acciona con un resorte para garantizar que de manera automática quede trabado en los dientes de la rueda dentada. Un malacate que sirve para enrollar un cable en un tambor debe tener un trinquete para impedir que el cable se desenrolle al levantar la palanca.
8.7.Bandas y cadenas de transmisión
Las bandas de transmisión son en esencia un par de cilindros giratorios con el movimiento de uno de ellos transfiriéndose al otro mediante una banda (Figura 8.22). En las bandas de transmisión se aprovecha la fricción que se crea entre las poleas montadas sobre los ejes y la banda que rodea el arco de contacto para transmitir un par motor. Dado que la transferencia se basa en las fuerzas de fricción, existe la posibilidad de un derrape o deslizamiento. El par motor transmitido se debe a las diferencias de tensión que se producen en la banda durante la operación. Esta diferencia ocasiona que en la banda haya un lado apretado y otro flojo. Si la tensión en la parte apretada es igual a T1 y la del lado flojo es T2, entonces la polea A de la Figura 8.22 es la polea conductora: par motor en A= (T1 – T2)Ra

donde rA es el radio de la polea A. Para la polea impulsada B se tiene que: par motor en B = (T1 – T2)rB donde rB es el radio de la polea B. Dado que la potencia transmitida es igual al producto del par motor y de la velocidad angular, y puesto que la velocidad angular es igual a v/rA para la polea A y v/rB para la polea B, donde v es la velocidad de la banda, entonces en cada polea tenemos: potencia = (T1 – T2)v En el método para transmitir potencia entre dos ejes, las bandas de transmisión tienen la ventaja de que la longitud de la banda se ajusta con facilidad para adaptarla a una amplia gama de distancias eje a eje, y proteger el sistema de manera automática de una sobrecarga, pues si la carga rebasa la tensión máxima que puede mantener gracias a las fuerzas de fricción, de inmediato se produce un deslizamiento. Si las distancias entre los ejes son grandes, es más conveniente usar bandas de transmisión que engranes; en cambio, para distancias de separación pequeñas es preferible usar engranes. Para obtener un efecto de engranaje se utilizan poleas de diferente tamaño. Sin embargo, la relación de engranaje está limitada alrededor de 3, debido a la necesidad de mantener un arco de contacto adecuado entre la banda y las poleas. La banda de transmisión de la Figura 8.22 hace girar la rueda impulsada en la misma dirección de la rueda impulsora. La Figura 8.23 muestra dos tipos de transmisiones inversoras. En las dos formas de transmisión, ambas caras de la banda están en contacto con las ruedas, por lo que no es posible utilizar bandas en V (bandas trapezoidales) ni bandas dentadas reguladoras de tiempo.

8.7.1 Tipos de bandas
Los cuatro tipos principales de bandas (Figura 8.24) son: 1. Plana El área transversal de esta banda es rectangular. La eficiencia de esta transmisión es casi 98% y produce poco ruido. Es capaz de transmitir la potencia en largas distancias entre los centros de las poleas. Las poleas con cejas se usan para impedir que las bandas se salgan de la guía. 2. Redonda La sección transversal es circular y se emplea con poleas con ranura. 3. En V Las bandas en V o trapezoidales se utilizan en poleas con ranura. Son menos eficientes que las bandas planas, aunque se pueden usar muchas de ellas en una sola rueda, por lo que es posible obtener una transmisión múltiple. 4. Banda dentada reguladora de tiempo Las bandas reguladoras de tiempo requieren ruedas dentadas en las que cada diente encaje en las ranuras de las ruedas. Esta banda, a diferencia de otras, no se estira ni se resbala, por lo que transmite potencia a una velocidad angular constante. Los dientes le permiten avanzar a velocidad lenta o rápida.

8.7.2 Cadenas
Para evitar deslizamientos se utilizan cadenas que se traban en los dientes de los cilindros rotacionales, lo que equivale a un par de engranes conectados. La relación de engranaje de una cadena es la misma que la de un tren de engranes. El mecanismo de transmisión de una bicicleta es un ejemplo de cadena de transmisión. Las cadenas permiten controlar varios ejes usando sólo una rueda, con lo que se logra una transmisión múltiple. No son tan silenciosas como la banda dentada reguladora de tiempo, pero se pueden usar en pares de rotación mayores.
8.8 Cojinetes (chumaceras)
Siempre que hay desplazamiento de una superficie que está en contacto con otra, ya sea por rotación o deslizamiento, las fuerzas de fricción producidas generan calor que desperdicia energía y produce desgaste. La función de los cojinetes o chumaceras (también conocidos como rodamientos) es guiar el movimiento de una parte respecto a otra con mínima fricción y máxima exactitud. Es de particular importancia la necesidad de proporcionar un soporte adecuado a los ejes rotacionales, es decir, un soporte a las cargas radiales. El término cojinete de empuje designa los cojinetes que permiten soportar fuerzas a lo largo de un eje cuando el movimiento relativo es una rotación. En las siguientes secciones se resumen las características de diversos tipos de chumaceras de uso común.
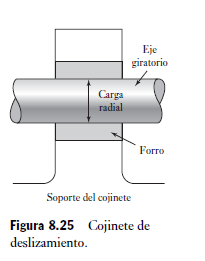
Los cojinetes se usan para apoyar ejes rotacionales que soportan carga en dirección radial. El cojinete consiste básicamente en una inserción de un material adecuado que se ajusta entre el eje y el soporte (Figura 8.25). Al girar el eje, la superficie del soporte se desliza sobre la superficie del cojinete. El inserto puede ser un metal blando, una aleación de aluminio, una aleación de cobre, bronce o un polímero como el nailon o el PTFE. Gracias al material insertado se reducen la fricción y el desgaste que se habrían producido si el eje hubiese girado en un orificio en el soporte. El cojinete puede operar en seco o lubricado. Plásticos como el nailon y el PTFE en general se utilizan sin lubricación, ya que su coeficiente de fricción es muy bajo. Un material muy utilizado para fabricar cojinetes es el bronce sinterizado, cuya estructura porosa permite que se impregne aceite y, de esta manera, el cojinete ya tiene un lubricante “incorporado”. La lubricación puede ser:
Figura 8.25 Cojinete de deslizamiento.
1. Hidrodinámica El cojinete con lubricación hidrodinámica tiene un eje que gira continuamente en aceite, de manera que su desplazamiento sólo se realiza en el aceite y no se apoya en el metal (Figura 8.26). La carga se soporta gracias a la presión que la rotación del eje genera en el aceite.
2. Hidrostática Un problema de la lubricación hidrodinámica es que el eje sólo se mueve en aceite cuando gira; pero si está en reposo, hay contacto metal a metal. Para evitar un excesivo desgaste durante el arranque y cuando la carga es baja, se bombea aceite al área del cojinete con presión suficiente para levantar el eje y mantenerlo separado del metal en condiciones de reposo.
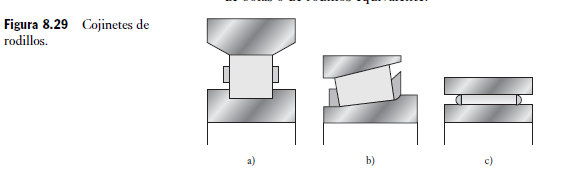
También hay varios tipos de cojinetes de rodillos; los siguientes son algunos ejemplos:
1. Rodillo cilíndrico (Figura 8.29a)) Es mejor para cargas radiales que el cojinete de bolas equivalente, pero en general no es recomendable para cargas axiales. Soportan cargas mayores que los cojinetes de bolas de las mismas dimensiones debido a su mayor área de contacto. Sin embargo, no permiten desalineamiento.
2. Rodillo cónico (Figura 8.29b)) Es bueno para cargas radiales y en una dirección para cargas axiales.
3. Rodillo de agujas (Figura 8.29c)) Su rodillo tiene una relación longitud/diámetro de valor elevado y tiende a usarse en situaciones donde no hay suficiente espacio para alojar el cojinete de bolas o de rodillos equivalente.
4. Capa límite Se trata de una delgada capa de lubricante que se adhiere a la superficie del cojinete.
8.8.2 Cojinetes de bolas y de rodillos
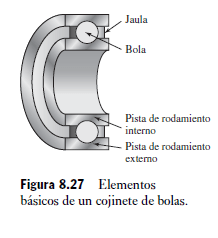
Con este tipo de cojinetes, la carga principal se transfiere del eje rotacional al apoyo mediante un contacto de rodadura en vez de un contacto por deslizamiento. Un cojinete de rotación consta de cuatro elementos principales: una pista interna, una pista externa, el elemento de rodamiento de bolas o rodillos y una jaula que mantiene separados los elementos de rodamiento (Figura 8.27). Las pistas de rodamiento internas y externas contienen guías endurecidas dentro de las cuales giran los elementos rodantes. Hay varios tipos de cojinetes de bolas:
1. Rígido de bolas (Figura 8.28a)). Este cojinete es bueno para soportar cargas radiales, aunque moderadamente bueno para soportar cargas axiales. Es un rodamiento versátil que se puede utilizar con una amplia gama de cargas y velocidades.
2. Ranura de relleno (Figura 8.28b)). Este cojinete soporta cargas radiales mayores que los rígidos de bolas, pero no se usan cuando hay cargas axiales.
3. Contacto angular (Figura 8.28c)). Es recomendable para cargas radiales y axiales y mejor aún para cargas axiales que el rígido de bolas.
4. De doble hilera (Figura 8.28d)). Los cojinetes de bolas de doble hilera se fabrican en diversos tipos y son capaces de soportar cargas radiales mayores que los de una hilera. En la figura se ilustra un cojinete de bolas de doble hilera con ranura profunda; existen versiones de doble hilera para cada una de las versiones de una hilera anteriores.
5. Cojinete auto alienable (Figura 8.28e)). Los cojinetes de una hilera pueden aceptar una ligera desalineación del eje, pero si la desalineación es considerable, debe usarse un cojinete corrector de holgura. Éste sólo tiene capacidad para soportar cargas radiales moderadas y es deficiente para cargas axiales.
6. Axiales (Figura 8.28f)). Están diseñados para soportar cargas axiales, aunque no son adecuados para cargas radiales.
8.8.3 Selección de los rodamientos
En general, los cojinetes de deslizamiento seco sólo se utilizan en ejes de diámetro pequeño con carga y velocidad también pequeños; los rodamientos de bolas y de rodillos, es decir, en los que hay movimiento rotacional, se usan para rangos mucho más amplios de diámetros de eje, cargas y velocidad más altas, y los rodamientos hidrodinámicos se usan para cargas y ejes de diámetro grandes.
Resumen
Los mecanismos son dispositivos que pueden considerarse convertidores de movimiento porque transforman el movimiento de una forma a otra forma requerida. Al movimiento de un cuerpo se le puede considerar una combinación de movimientos de rotación y de traslación. El número de grados de libertad es el número de componentes al movimiento que son requeridos para generar el movimiento. Cada parte de un mecanismo que tiene movimiento relativo a alguna otra parte es conocido como articulación. A los puntos de unión de una articulación con los puntos de otras se les llama nodos. Una unión es una conexión entre dos o más articulaciones en sus nodos. A una secuencia de uniones y articulaciones se le conoce como cadena cinemática. Una cadena de cuatro barras consiste de cuatro articulaciones conectadas para dar cuatro uniones en las que se pueda realizar un giro. Una leva es un cuerpo que gira u oscila y al hacer esto difunde un movimiento reciprocante u oscilatorio a un segundo cuerpo llamado seguidor, con el que está en contacto.
Los engranes se pueden utilizar para la transmisión del movimiento rotatorio entre los ejes paralelos y para los ejes cuyos ejes están inclinados entre sí. Los sistemas de piñón y cremallera y de tornillo y tuerca se pueden emplear para convertir el movimiento de rotación a movimiento de traslación. Los trinquetes se usan para asegurar o detener un mecanismo cuando está sosteniendo una carga. La banda y la cadena de transmisión se pueden usar para transmitir el movimiento rotatorio entre ejes que son paralelos y tienen alguna distancia. Los cojinetes se utilizan para guiar con la mínima fricción y la máxima exactitud el movimiento de una pieza con relación a otra.
Problemas
8.1 Explique los términos:
a) mecanismo,
b) cadena cinemática. 8.2 Explique qué es una cadena de cuatro barras. 8.3 Después de analizar los siguientes mecanismos, indique los grados de libertad de cada uno:
a) E l mecanismo de la bisagra del cofre de un automóvil.
b) E l mecanismo de la puerta trasera de una camioneta.
c) El mecanismo del limpiaparabrisas.
d) Su rodilla
e) Su tobillo.
8.4 Analice el movimiento de los siguientes mecanismos e indique si hay rotación pura, traslación pura o es una combinación de componentes de rotación y traslación.
a) Las teclas en el teclado de una computadora.
b) La pluma de un graficador XY (plotter).
c) La manecilla de un reloj.
d) La aguja de un amperímetro de bobina móvil.
e) Un desarmador automático.
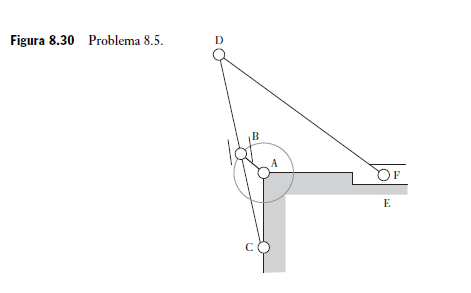
8.5 En el mecanismo de la Figura 8.30, el brazo AB gira a velocidad constante. B y F son guías de deslizamiento que van de CD y de AF. Describa el comportamiento de este mecanismo.
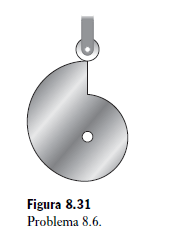
8.6 Explique cómo variará el desplazamiento de la leva-seguidor de la Figura 8.31 con el ángulo de rotación de la leva.
8.7 Una leva circular con diámetro de 100 mm tiene un eje de rotación excéntrico desviado unos 30 mm del centro. Cuando se usa con un seguidor tipo cuchillo y su línea de acción pasa por el centro de rotación, ¿cuál será la diferencia entre los desplazamientos máximo y mínimo del seguidor?
8.8 Diseñe un sistema de leva-seguidor que produzca velocidades de seguidor constantes cuando los desplazamientos del seguidor varíen entre 40 y 100 mm.
8.9 Diseñe un sistema mecánico que sirva para:
a) Operar una secuencia de microinterruptores de acuerdo con una secuencia programada.
b) Mover una herramienta a velocidad constante en una dirección y luego rápidamente regresarla a su posición inicial.
c) Transformar una rotación en un movimiento lineal de avance y retroceso con movimiento armónico simple.
d) Transformar una rotación con cierta abertura angular en un desplazamiento lineal.
e) Transformar la rotación de un eje en la rotación de otro eje paralelo a determinada distancia del primero.
f) Transformar la rotación de un eje en la rotación de otro eje cercano en posición perpendicular respecto al primero.
8.10 Un tren de engranes compuesto consta de un engrane final impulsado con 15 dientes conectado a otro engrane con 90 dientes. En el mismo eje del segundo engrane hay un engrane con 15 dientes; éste se conecta con un cuarto engrane, que es el engrane motriz con 60 dientes, ¿cuál es la relación de engranaje total?